首先导入所需要的库文件

1
2
3

import matplotlib.pyplot as plt  # 导入可视化库
import numpy as np               # 导入数据处理库
from sklearn import datasets     # 导入sklearn自带的数据集

把我们的参数值求解公式$\theta=(X^TX)^{-1}X^TY$转换为代码

def fit(self, X, y):                    # 训练集的拟合
        X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
        print (X.shape)        
        X_ = np.linalg.inv(X.T.dot(X))  # 公式求解 -- X.T表示转置，X.dot(Y)表示矩阵相乘
        self.w = X_.dot(X.T).dot(y)     # 返回theta的值

其中：$(X^TX)^{-1} $表示为：

1 2	X_ = np.linalg.inv(X.T.dot(X)) # 公式求解 -- X.T表示转置，X.dot(Y)表示矩阵相乘 np.linalg.inv() 表示求逆矩阵

其中：$X^TY $表示为：

1	X.T.dot(X)

所以完整公式$\theta=(X^TX)^{-1}X^TY$表示为：

1	X_.dot(X.T).dot(y)

由于我们最终得到的线性回归函数是$y=\theta x+b$即预测函数：

def predict(self, X):               # 测试集的测试反馈
                                    # 为偏置权值插入常数项
    X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
    y_pred = X.dot(self.w)          # 测试集与拟合的训练集相乘
    return y_pred                   # 返回最终的预测值

其中得到的预测结果y_pred=X_text$\cdot\theta$

1	y_pred = X.dot(self.w) # 测试集与参数值相乘

最终得出线性回归代码：

class LinearRegression():
    def __init__(self):          # 新建变量
        self.w = None

    def fit(self, X, y):         # 训练集的拟合
        X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
        print (X.shape)        
        X_ = np.linalg.inv(X.T.dot(X))  # 公式求解 -- X.T表示转置，X.dot(Y)表示矩阵相乘
        self.w = X_.dot(X.T).dot(y)     # 返回theta的值

    def predict(self, X):               # 测试集的测试反馈
                                        # 为偏置权值插入常数项
        X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
        y_pred = X.dot(self.w)          # 测试集与拟合的训练集相乘
        return y_pred                   # 返回最终的预测值

同时我们需要得出预测值与真实值的一个平方平均值

def mean_squared_error(y_true, y_pred):
                                        #真实数据与预测数据之间的差值（平方平均）
    mse = np.mean(np.power(y_true - y_pred, 2))
    return mse

最后就是进行我数据的加载，训练，测试过程以及可视化

def main():
    # 第一步：导入数据
    # 加载糖尿病数据集
    
    diabetes = datasets.load_diabetes()
    # 只使用其中一个特征值
    X = diabetes.data[:, np.newaxis, 2]
    print (X.shape)

    #第二步：将数据分为训练集以及测试集
    x_train, x_test = X[:-20], X[-20:]
    y_train, y_test = diabetes.target[:-20], diabetes.target[-20:]

    #第三步：导入线性回归类（之前定义的）
    clf = LinearRegression()
    clf.fit(x_train, y_train)    # 训练
    y_pred = clf.predict(x_test) # 测试

    #第四步：测试误差计算（需要引入一个函数）
    # 打印平均值平方误差
    print ("Mean Squared Error:", mean_squared_error(y_test, y_pred))

    #matplotlib可视化输出
    # Plot the results
    plt.scatter(x_test[:,0], y_test,  color='black')         # 散点输出
    plt.plot(x_test[:,0], y_pred, color='blue', linewidth=3) # 预测输出
    plt.show()

可视化结果

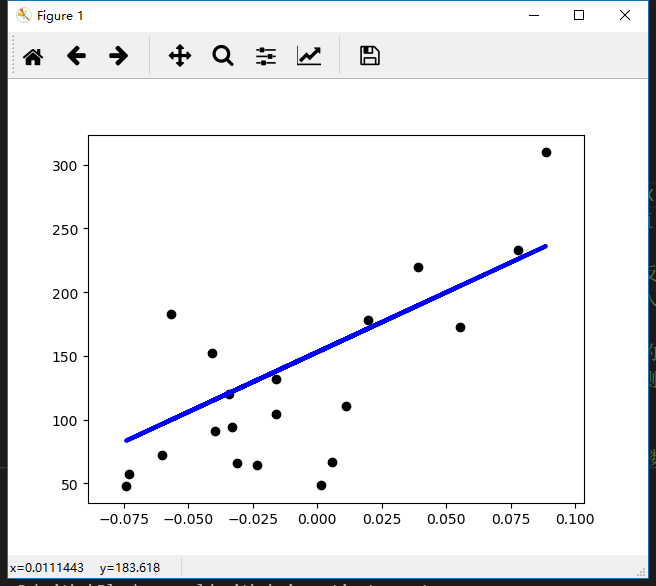
完整线性回归的代码

import matplotlib.pyplot as plt  # 导入可视化库
import numpy as np               # 导入数据处理库
from sklearn import datasets     # 导入sklearn自带的数据集
import csv

class LinearRegression():
    def __init__(self):          # 新建变量
        self.w = None

    def fit(self, X, y):         # 训练集的拟合
        X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
        print (X.shape)        
        X_ = np.linalg.inv(X.T.dot(X))  # 公式求解 -- X.T表示转置，X.dot(Y)表示矩阵相乘
        self.w = X_.dot(X.T).dot(y)     # 返回theta的值

    def predict(self, X):               # 测试集的测试反馈
                                        # 为偏置权值插入常数项
        X = np.insert(X, 0, 1, axis=1)  # 增加一个维度
        y_pred = X.dot(self.w)          # 测试集与拟合的训练集相乘
        return y_pred                   # 返回最终的预测值

def mean_squared_error(y_true, y_pred):
                                        #真实数据与预测数据之间的差值（平方平均）
    mse = np.mean(np.power(y_true - y_pred, 2))
    return mse

def main():
    # 第一步：导入数据
    # 加载糖尿病数据集
    diabetes = datasets.load_diabetes()
    # 只使用其中一个特征值(把一个422x10的矩阵提取其中一列变成422x1)
    X = diabetes.data[:, np.newaxis, 2]  # np.newaxis的作用就是在原来的数组上增加一个维度。2表示提取第三列数据
    print (X.shape)

    # 第二步：将数据分为训练集以及测试集
    x_train, x_test = X[:-20], X[-20:]
    print(x_train.shape,x_test.shape)  # (422, 1) (20, 1)
    # 将目标分为训练/测试集合
    y_train, y_test = diabetes.target[:-20], diabetes.target[-20:]
    print(y_train.shape,y_test.shape)  # (422,) (20,)

    #第三步：导入线性回归类（之前定义的）
    clf = LinearRegression()
    clf.fit(x_train, y_train)    # 训练
    y_pred = clf.predict(x_test) # 测试

    #第四步：测试误差计算（需要引入一个函数）
    # 打印平均值平方误差
    print ("Mean Squared Error:", mean_squared_error(y_test, y_pred))  # Mean Squared Error: 2548.072398725972

    #matplotlib可视化输出
    # Plot the results
    plt.scatter(x_test[:,0], y_test,  color='black')         # 散点输出
    plt.plot(x_test[:,0], y_pred, color='blue', linewidth=3) # 预测输出
    plt.show()

if __name__ == '__main__':
    main()

转载请注明：Seven的博客 » 点击阅读原文