生成对抗网络
生成式对抗网络(GAN, Generative Adversarial Networks )是一种深度学习模型,是近年来复杂分布上无监督学习最具前景的方法之一。
模型通过框架中(至少)两个模块:生成模型(Generative Model)和判别模型(Discriminative Model)的互相博弈学习产生相当好的输出。
原始 GAN 理论中,并不要求 G 和 D 都是神经网络,只需要是能拟合相应生成和判别的函数即可。
但实用中一般均使用深度神经网络作为 G 和 D 。一个优秀的GAN应用需要有良好的训练方法,否则可能由于神经网络模型的自由性而导致输出不理想。
GAN的基本框架
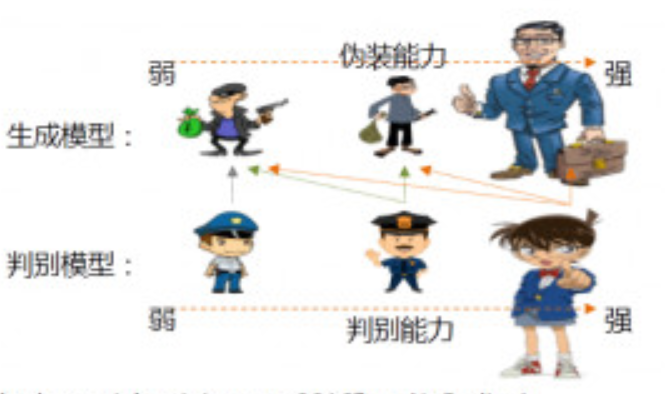
GAN所建立的一个学习框架,实际上我们可以看成生成模型和判别模型之间的一个模拟对抗游戏。我们可以把生成模型看作一个伪装者,而把判别模型看成一个警察。生成模型通过不断地学习来提高自己的伪装能力,从而使得生成出来的数据能够更好地“欺骗”判别模型。而判别模型则通过不断的训练来提高自己的判别能力,能够更准确地判断出数据的来源。GAN就是这样一个不断对抗的网络。GAN的架构如下图所示:
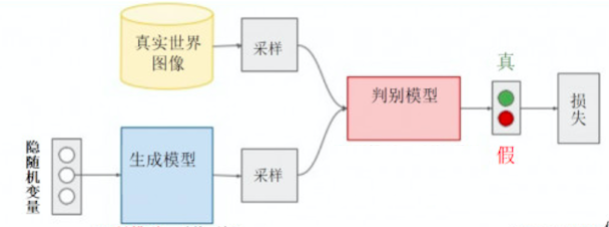
生成模型以随机变量作为输入,其输出是对真实数据分布的一个估计。
生成数据和真实数据的采样都由判别模型进行判别,并给出真假性的判断和当前的损失。
利用反向传播,GAN对生成模型和判别模型进行交替优化。
GAN的优化目标
在对抗生成网络中,有两个博弈的角色分别为生成式模型(generative model)和判别式模型(discriminative model)。具体方式为:
- 生成模型G捕捉样本数据的分布,判别模型D时一个二分类器,估计一个样本来自于训练数据(而非生成数据)的概率。
在博弈的过程中我们需要提高两个模型的能力,所以通过不断调整生成模型G和判别模型D,直到判别模型D不能把数据的真假判别出来为止。在调整优化的过程中,我们需要:
- 优化生成模型G,使得判别模型D无法判别出来事件的真假。
- 优化判别模型D,使得它尽可能的判别出事件的真假。
举个栗子:
假设数据的概率分布为M,但是我们不知道具体的分布和构造是什么样的,就好像是一个黑盒子。为了了解这个黑盒子,我们就可以构建一个对抗生成网络:
- 生成模型G:使用一种我们完全知道的概率分布N来不断学习成为我们不知道的概率分布M.
- 判别模型D:用来判别这个不断学习的概率是我们知道的概率分布N还是我们不知道的概率分布M。
我们用图像来体现:
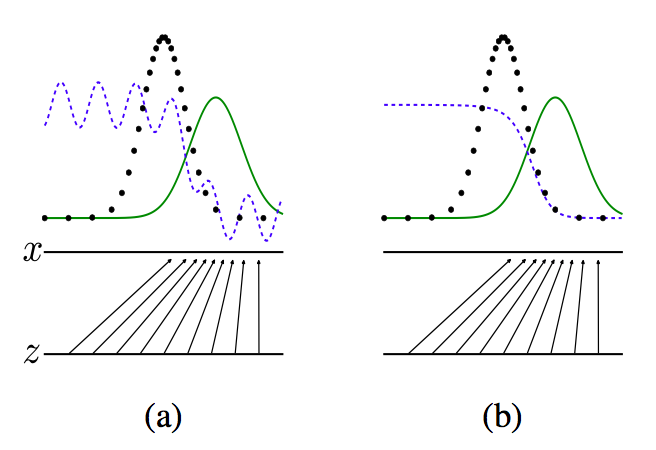
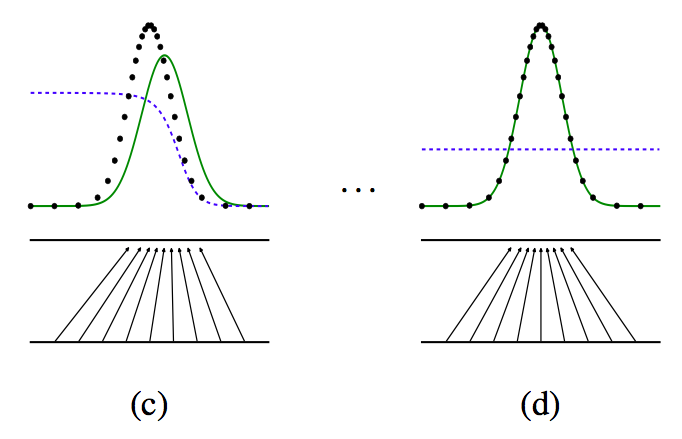
由上图所示:
- 黑点所组成的数据分布是我们所不知道的概率分布M所形成的
- 绿色的线表示生成模型G使用已知的数据和判别模型不断对抗生成的数据分布。
- 蓝色的线表示判断模型D
- a图:初始状态
- b图:生成模型不变,优化判别模型,直到判别的准确率最高
- c图:判别模型不变。优化生成模型。直到生成的数据的真实性越高
- d图:多次迭代后,生成模型产生的数据和概率部分M的数据基本一致,从而判别模型认为生成模型生成的数据就是概率分布M的数据分布。
GAN的数学推导
符号定义:
定义判别模型和生成模型:
$E_{x \sim P_{data}}(x) \cdot logD(x)$
由上式可知:当$x \sim P_{data}(x) , D(x)=1 $的时,$E_{x \sim P_{data}}(x)$取得最大值。
$E_{x \sim P_{z}}(z) \cdot log(1-D(G(z)))$
由上式可知:当$x \sim P_{z}(z) , D(G(z))=0 $的时,$E_{x \sim P_{z}}(z)$取得最大值。
所以为了我们的判别模型越来越好,能力越来越强大,定义目标函数为:
$V(G,D)= logD(x) + log(1-D(G(z)))$
要使判别模型取得最好,所以需要使$V(G,D)$取得最大,即:
$D = agrmax_DV(G,D)$
当判别模型最好的时候,最好的生成模型就是目标函数取得最小的时候:
$G=argmin_G(aggmax_D(V(G, D)))$
所以经过这一系列的讨论,这个问题就变成了最大最小的问题,即:
$min_Gmax_DV(G, D)=E_{x \sim P_{data}}(x) \cdot logD(x)+ E_{x \sim P_{z}}(z) \cdot log(1-D(G(z)))$
最优判别模型:
最终的目标函数:
$V(G,D)= \int_x P_{data}(x) \cdot logD(x) + P_g(x)log(1-D(G(z))) d(x)$
令:$V(G,D)=f(y), P_{data}(x)=a, P_g(x)=b$
所以:$f(y)=alogy+blog(1-y)$
因为:$a+b \ne 0$
所以最大值:$\frac{a}{a+b}$
最后,我们得到的最优判别模型就是:
$D(x)=\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}$
由于生成对抗网络的目的是:得到生成模型可以生成非常逼真的数据,也就是说是和真实数据的分布是一样的。因此最优的判别模型的输出为:
$D(x)=\frac{P_{data}}{P_{data}+P_g}=\frac12$
其中:$P_g和P_{data}$的数据分布是一样的。
也就是说当D输出为0.5时,说明鉴别模型已经完全分不清真实数据和GAN生成的数据了,此时就是得到了最优生成模型了。
证明生成模型:
充分性:
前面我们已经得到了最优的判别模型,我们直接把数据带进目标函数:
$V(G)=\int_x [P_{data}(x) \cdot log(\frac 12) + P_g(x)log(\frac 12) ]d(x) =-log4$
必要性:
$V(G)=\int_x [P_{data}(x) \cdot log(\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}) + P_g(x)log(1-\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}) ] d(x) $
$V(G)=\int_x [(log2-log2)\cdot P_{data}(x)+P_{data}(x) \cdot log(\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}) + (log2-log2)\cdot P_g(x) + P_g(x)log(1-\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}) ]d(x) $
$V(G)=-log2 \int_x [P_g(x) +P_{data}(x)]d(x)+\int_x [P_{data}(x) \cdot(log2+ log(\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}))+ P_g(x) \cdot (log2+log(1-\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}) )] d(x)$
$V(G)=-log4+\int_x [P_{data}(x) \cdot log(\frac{P_{data}(X)}{P_{data}(X)+\frac{P_g(x)}{2}}) + P_g(x)log(1-\frac{P_{data}(X)}{P_{data}(X)+\frac{P_g(x)}{2}}) ] d(x) $
我们把最终结果转换为KL散度:
$V(G)=-log4+KL(P_{data} \mid \frac{P_{data}+P_g}{2})+KL(P_g \mid \frac{P_{data}+P_g}{2} )$
因为:KL散度永远大于等于0,所以可以知道目标函数最终最优值为-log4。
GAN的特性
优点:
- 模型优化只用到了反向传播,而不需要马尔科夫链。
- 训练时不需要对隐变量做推断。
- 理论上,只要是可微分函数都能用于构建生成模型G和判别模型D,因而能够与深度神经网络结合–>深度产生式模型。
- 生成模型G的参数更新不是直接来自于数据样本,而是使用来自判别模型D的反向传播梯度。
缺点:
- 可解释性差,生成模型的分布没有显示的表达。它只是一个黑盒子一样的映射函数:输入是一个随机变量,输出是我们想要的一个数据分布。
- 比较难训练,生成模型D和判别模型G之间需要很好的同步。例如,在实际中我们常常需要 D 更新 K次, G 才能更新 1 次,如果没有很好地平衡这两个部件的优化,那么G最后就极大可能会坍缩到一个鞍点。
转载请注明:Seven的博客

