递归神经网络之python实现RNN算法

发表于 | 分类于 | | 阅读次数: |
字数统计: 923 | 阅读时长 ≈ 4
卷积神经网络，python手写，RNN, 实现卷积神经网络

PYTHON实现RNN算法

实现学习二进制的加法。

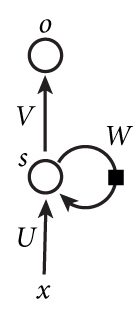
images

如上图所示，我们来手写RNN算法：

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2018/8/29 13:51
# @Author  : Seven
# @Site    :
# @File    : demo.py
# @Software: PyCharm

# TODO:导入环境
import copy
import numpy as np
np.random.seed(0)


# 使用SIGMOD函数转换成非线性
def sigmoid(inputs):
    output = 1 / (1 + np.exp(-inputs))
    return output


# 将SIGMOD函数的输出转换成其导数
def sigmoid_output_to_derivative(output):
    return output * (1 - output)


# TODO: 生成训练数据集-->把十进制转换为8位二进制
int2binary = {}
binary_dim = 8

largest_number = pow(2, binary_dim)  # 2**8=256

# 把0-256转换成对应的二进制编码并储存起来
binary = np.unpackbits(
    np.array([range(largest_number)], dtype=np.uint8).T, axis=1)

for i in range(largest_number):
    int2binary[i] = binary[i]

# 参数定义
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1

# 初始化权重参数--在-1到1之间
U = 2 * np.random.random((input_dim, hidden_dim)) - 1
V = 2 * np.random.random((hidden_dim, output_dim)) - 1
W = 2 * np.random.random((hidden_dim, hidden_dim)) - 1

# 更新权重参数
U_update = np.zeros_like(U)
V_update = np.zeros_like(V)
W_update = np.zeros_like(W)

# TODO:训练
for step in range(10000):

    # 随机生成一个加法a+b=c（因为最大是8位，所以a最大是largest_number的1/2）
    a_int = np.random.randint(largest_number / 2)  # int version
    a = int2binary[a_int]  # binary encoding

    b_int = np.random.randint(largest_number / 2)  # int version
    b = int2binary[b_int]  # binary encoding

    # true answer
    c_int = a_int + b_int
    c = int2binary[c_int]

    # 存储概率最大的二进制--预测值
    d = np.zeros_like(c)

    overallError = 0

    out_deltas = list()
    layer_1_values = list()  # 保存’记忆‘
    layer_1_values.append(np.zeros(hidden_dim))

    # 沿着二进制的位置移动--前向传播
    for position in range(binary_dim):
        # 生成输入和输出的值
        X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
        y = np.array([c[binary_dim - position - 1]]).T

        # hidden layer --> UX+layer1·W
        layer_1 = sigmoid(np.dot(X, U) + np.dot(layer_1_values[-1], W))

        # output layer
        layer_2 = sigmoid(np.dot(layer_1, V))

        # 计算损失值
        layer_2_error = y - layer_2
        out_deltas.append(layer_2_error * sigmoid_output_to_derivative(layer_2))
        overallError += np.abs(layer_2_error[0])

        # 解码成十进制
        d[binary_dim - position - 1] = np.round(layer_2[0][0])

        # 保存记忆，以便下一时刻使用
        layer_1_values.append(copy.deepcopy(layer_1))

    future_layer_1_delta = np.zeros(hidden_dim)

    # 反向传播
    for position in range(binary_dim):
        X = np.array([[a[position], b[position]]])
        layer_1 = layer_1_values[-position - 1]
        prev_layer_1 = layer_1_values[-position - 2]

        # error at output layer
        layer_2_delta = out_deltas[-position - 1]
        # error at hidden layer
        layer_1_delta = (future_layer_1_delta.dot(W.T) + layer_2_delta.dot(
            V.T)) * sigmoid_output_to_derivative(layer_1)

        # 更新权重参数
        V_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        W_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        U_update += X.T.dot(layer_1_delta)

        future_layer_1_delta = layer_1_delta

    U += U_update * alpha
    V += V_update * alpha
    W += W_update * alpha

    U_update *= 0
    V_update *= 0
    W_update *= 0

    # print out progress
    if step % 1000 == 0:
        print("错误值:" + str(overallError))
        print("预测值:" + str(d))
        print("正确值:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")

结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
损失值:[3.45638663]
预测值:[0 0 0 0 0 0 0 1]
正确值:[0 1 0 0 0 1 0 1]
9 + 60 = 1
------------
损失值:[3.63389116]
预测值:[1 1 1 1 1 1 1 1]
正确值:[0 0 1 1 1 1 1 1]
28 + 35 = 255
------------
损失值:[3.91366595]
预测值:[0 1 0 0 1 0 0 0]
正确值:[1 0 1 0 0 0 0 0]
116 + 44 = 72
------------
损失值:[3.72191702]
预测值:[1 1 0 1 1 1 1 1]
正确值:[0 1 0 0 1 1 0 1]
4 + 73 = 223
------------
损失值:[3.5852713]
预测值:[0 0 0 0 1 0 0 0]
正确值:[0 1 0 1 0 0 1 0]
71 + 11 = 8
------------
损失值:[2.53352328]
预测值:[1 0 1 0 0 0 1 0]
正确值:[1 1 0 0 0 0 1 0]
81 + 113 = 162
------------
损失值:[0.57691441]
预测值:[0 1 0 1 0 0 0 1]
正确值:[0 1 0 1 0 0 0 1]
81 + 0 = 81
------------
损失值:[1.42589952]
预测值:[1 0 0 0 0 0 0 1]
正确值:[1 0 0 0 0 0 0 1]
4 + 125 = 129
------------
损失值:[0.47477457]
预测值:[0 0 1 1 1 0 0 0]
正确值:[0 0 1 1 1 0 0 0]
39 + 17 = 56
------------
损失值:[0.21595037]
预测值:[0 0 0 0 1 1 1 0]
正确值:[0 0 0 0 1 1 1 0]
11 + 3 = 14
------------

转载请注明：Seven的博客

本文标题:递归神经网络之python实现RNN算法

文章作者:Seven

发布时间:2018年08月29日 - 00:00:00

最后更新:2018年12月11日 - 22:10:26

原始链接:http://yoursite.com/2018/08/29/2018-08-29-DL-RNN-hand/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

------ 本文结束------
坚持原创技术分享，您的支持将鼓励我继续创作！
0%