递归神经网络之BackPropagation Through Time

循环神经网络的训练算法：BPTT

BackPropagation Through Time (BPTT)经常出现用于学习递归神经网络（RNN）。

与前馈神经网络相比，RNN的特点是可以处理过去很长的信息。因此特别适合顺序模型。

BPTT扩展了普通的BP算法来适应递归神经网络。

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

前向计算每个神经元的输出值；
反向计算每个神经元的误差项$E$值，它是误差函数E对神经元的加权输入的偏导数；
计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。

前向计算

网络结构：

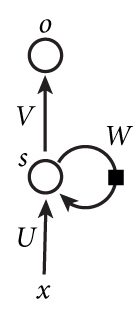
images

由图可知：

INPUT LAYER -->HIDDEN LAYER：$S_t=tanh(U \cdot X_t+W \cdot S_{t-1}) $
HIDDEN LAYER --> OUTPUT LAYER：$y_t = softmax(V \cdot S_t)$

损失函数

我们将损失或者误差定义为交叉熵损失：

$E_t(y_t,\widehat y_t) = -y_t \cdot log\widehat y_t$

$E(y_t,\widehat y_t) = -\sum_t y_t \cdot log\widehat y_t$

注意:

$y_t$：是t时刻的正确值
$\widehat y_t$：是我们的预测值
总误差是每个时刻的误差之和

反向计算

循环层如下图所示：

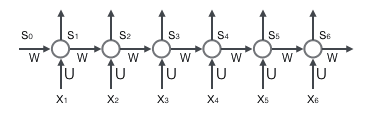
images

接下来，我们就需要使用链式法则进行反向梯度的参数更新：

$\bigtriangleup U=\frac{ \partial E}{\partial U} = \sum_t \frac{\partial E_t}{\partial U}$
$\bigtriangleup W=\frac{ \partial E}{\partial W} = \sum_t \frac{\partial E_t}{\partial W}$
$\bigtriangleup V=\frac{ \partial E}{\partial V} = \sum_t \frac{\partial E_t}{\partial V}$

我们令$t=3$为栗子：

$\bigtriangleup V=\frac{ \partial E_3}{\partial V} = \frac{\partial E_3}{\partial \widehat y_3} \cdot \frac{\partial \widehat y_3}{\partial net_3} \cdot \frac{\partial net_3}{\partial V} = (\widehat y_3 - y_3) \otimes S_3$

注意：$net_3=V \cdot S_3$，$\otimes$是外积，V只和当前的时间有关，所以计算非常简单。

$\bigtriangleup W=\frac{ \partial E_3}{\partial W} = \frac{\partial E_3}{\partial \widehat y_3} \cdot \frac{\partial \widehat y_3}{\partial S_3} \cdot \frac{\partial S_3}{\partial W} $

因为：

$S_3 = tanh(U \cdot X_t+W \cdot S_2)$，取决于$S_2$，而$S_2$又依赖于$W、S_1$。

所以:

$\bigtriangleup W=\frac{ \partial E_3}{\partial W} =\sum_{k=0}^3 \frac{\partial E_3}{\partial \widehat y_3} \cdot \frac{\partial \widehat y_3}{\partial S_3} \cdot \frac{\partial S_3}{\partial S_k} \cdot \frac{\partial S_k}{\partial net_k} \cdot \frac{\partial net_k}{\partial W} $

总结：W 在每一步中都有使用，所以我们需要$t=3$通过网络反向传播到$t=0$：

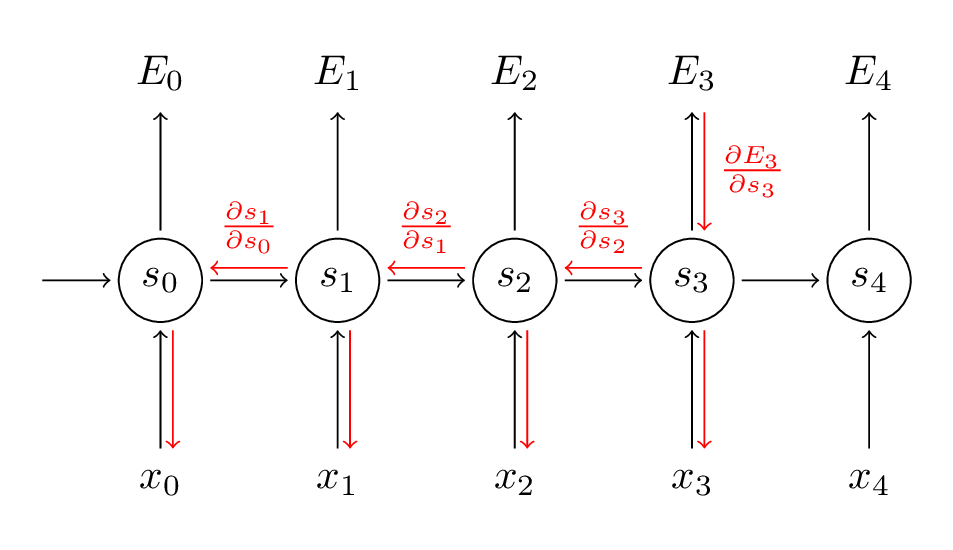
images

注意：这种方式是和我们前面所推导的深度神经网络的反向传播算法和卷积神经网络的反向传播算法是完全相同的。关键的区别就是我们总结了W的每个时刻的渐变，在传统的神经网络中，我们不跨层共享参数，因此我们不需要总结任何东西。

$\bigtriangleup U=\frac{ \partial E_3}{\partial U} =\sum_{k=0}^3 \frac{\partial E_3}{\partial \widehat y_3} \cdot \frac{\partial \widehat y_3}{\partial S_3} \cdot \frac{\partial S_3}{\partial S_k} \cdot \frac{\partial S_k}{\partial net_k} \cdot \frac{\partial net_k}{\partial U} $

总结：U参数W参数的传递过程基本一致。

参数更新

$U_{new}=U_{old}-\eta \bigtriangleup U$
$V_{new}=V_{old}-\eta \bigtriangleup V$
$W_{new}=W_{old}-\eta \bigtriangleup W$

$\eta$：学习率

梯度消失和梯度爆炸

RNN在训练中很容易发生梯度爆炸和梯度消失，这导致训练时梯度不能在较长序列中一直传递下去，从而使RNN无法捕捉到长距离的影响。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会收到NaN错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域。
使用relu代替sigmoid和tanh作为激活函数。
使用其他结构的RNNs，比如长短时记忆网络（LTSM）和Gated Recurrent Unit（GRU），这是最流行的做法。

转载请注明：Seven的博客