回顾DNN的反向传播算法
需要在理解深度神经网络的反向传播算来做预先理解,见神经网络入门-反向传播所总结的反向传播四部曲:
反向传播的四项基本原则:
基本形式:
$\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \times \sigma^{\prime}(net_i^{(L)}) $
$\delta^{(l)} = \sum_j \delta_j^{(l+1)} w_{ji}^{(l+1)} \sigma^{\prime}(net_i^{(l)})$
$\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\delta_i^{(l)}$
$\frac{\partial E_{total}}{\partial w_{ij}^{(l)}}=outh_j^{(l-1)}\delta_i^{(l)}$
矩阵形式:
$\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \bigodot \sigma^{\prime}(net_i^{(L)}) $ , $\bigodot$是Hadamard乘积(对应位置相乘)
$\delta^{(l)} = (w^{(l+1)})^T \delta^{(l+1)} \bigodot \sigma^{\prime}(net^{(l)})$
$\frac{\partial E_{total}}{\partial bias^{(l)}}=\delta^{(l)}$
$\frac{\partial E_{total}}{\partial w^{(l)}}=\delta^{(l)}(outh^{(l-1)})^T$
现在我们想把同样的思想用到卷积神经网络中,但是很明显,CNN有很多不同的地方(卷积计算层,池化层),不能直接去套用DNN的反向传播公式。
卷积神经网络的反向传播算法
卷积神经网络相比于多层感知机,增加了两种新的层次——卷积层与池化层。由于反向传播链的存在,要求出这两种层结构的梯度,仅需要解决输出对权值的梯度即可。 接下来我们根据卷积神经网络的网络结构来更新反向传播四部曲。
我们在推导DNN的反向传播的时候,推导过程中使用了:
$output^{(l+1)}=\sigma(W \cdot output^{(l)}+b)$
而对于卷积神经网络,我们使用卷积和池化的公式进行重新推导:
卷积层:$output^{(l+1)}=\sigma( output^{(l)}*W+b)$
池化层:$output^{(l+1)}=subsampling( output^{(l)}+b)$
卷积层
我们在回忆下:
$\delta^{(l)}=\frac{\partial E_{total}}{\partial net^{(l)}} $
$= \frac{\partial E_{total}}{\partial net^{(l+1)}} \cdot \frac{\partial net^{(l+1)}}{\partial net^{(l)}}$
$= \delta^{(l+1)} \times \frac{\partial (output^{(l)}*W+b)}{\partial net^{(l)}}$
$= \delta^{(l+1)} \times \frac{\partial (output^{(l)}*W+b)}{\partial out^{(l)}} \times \frac{\partial out^{(l)}}{\partial net^{(l)}}$
$= \delta^{(l+1)} \cdot \frac{\partial (output^{(l)}*W+b)}{\partial out^{(l)}} \cdot \sigma^{\prime}(net_i^{(L)})$
接下来,就是计算卷积运算的求导:
$\frac{\partial (output^{(l)}*W+b)}{\partial out^{(l)}}$
假如我们要处理如下的卷积操作:
$\left( \begin{array}{ccc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{array} \right) * \left( \begin{array}{ccc} w_{11}&w_{12} \\ w_{21}&w_{22} \end{array} \right) = \left( \begin{array}{ccc} z_{11}&z_{12} \\ z_{21}&z_{22} \end{array} \right)$
从这步操作来看,套用DNN反向传播的思想是行不通的,所以我们需要把卷积操作表示成如下等式。
$z_{11} = a_{11}w_{11} + a_{12}w_{12} + a_{21}w_{21} + a_{22}w_{22} \\ z_{12} = a_{12}w_{11} + a_{13}w_{12} + a_{22}w_{21} + a_{23}w_{22} \\ z_{21} = a_{21}w_{11} + a_{22}w_{12} + a_{31}w_{21} + a_{32}w_{22} \\ z_{22} = a_{22}w_{11} + a_{23}w_{12} + a_{32}w_{21} + a_{33}w_{22}$
对每个元素进行求导:
$\begin{align} \nabla a_{11} = & \frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial a_{11}}+ \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial a_{11}}+ \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial a_{11}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial a_{11}} \notag \\ =&w_{11} \notag \end{align}$
$\begin{align} \nabla a_{12} =& \frac{\partial C}{\partial z_{11}}\frac{\partial z_{11}}{\partial a_{12}} + \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial a_{12}} + \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial a_{12}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial a_{12}} \notag \\ =&w_{12} +w_{11} \notag \end{align}$
同理可得其他的$\nabla a_{ij}$,当你求出全部的结果后,你会发现我们可以用一个卷积运算来解决(实际就是把原来的卷积核做了180°的转换):
$\left( \begin{array}{ccc} 0&0&0&0 \\ 0&\ 1& 1&0 \\ 0&1 &1&0 \\ 0&0&0&0 \end{array} \right) * \left( \begin{array}{ccc} w_{22}&w_{21}\\ w_{12}&w_{11} \end{array} \right) = \left( \begin{array}{ccc} \nabla a_{11}&\nabla a_{12}&\nabla a_{13} \\ \nabla a_{21}&\nabla a_{22}&\nabla a_{23}\\ \nabla a_{31}&\nabla a_{32}&\nabla a_{33} \end{array} \right)$
最终我们就可以得到:
$\frac{\partial (output^{(l)}W+b)}{\partial out^{(l)}} =\left( \begin{array}{ccc} 0&0&0&0 \\ 0&\ 1& 1&0 \\ 0&1 &1&0 \\ 0&0&0&0 \end{array} \right) \left( \begin{array}{ccc} w_{22}&w_{21}\\ w_{12}&w_{11} \end{array} \right) $
所以原来的$\delta^{(l)} = (w^{(l+1)}) \delta^{(l+1)} \bigodot \sigma^{\prime}(net^{(l)})$就变为:
$\delta^{(l)} = (w^{(l+1)}) *rot180(W) \bigodot \sigma^{\prime}(net^{(l)})$
对于偏置项:
原来的是:$\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\delta_i^{(l)}$
因为对于全连接网络:$b, \delta^{(l)} \in R(n_{out}^{(l)})$
而对于卷积神经网络:$b \in R(n_{out}^{(l)}), \delta^{(l)} \in R(H_{out}^{(l)}, W_{out}^{(l)}, n_{out}^{(l)})$
我们对应的处理方式就是:
将$\delta^{(l)}$的H和W维度求和
所以:
$\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\sum_H \sum_W \delta_{(H,W,i)}^{(l)}$
卷积神经网络反向传播的四部曲
$\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \times \sigma^{\prime}(net_i^{(L)}) $
$\delta^{(l)} = (w^{(l+1)}) *rot180(W) \bigodot \sigma^{\prime}(net^{(l)})$
$\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\sum_H \sum_W \delta_{(H,W,i)}^{(l)}$
$\frac{\partial E_{total}}{\partial w^{(l)}}=rot180(\delta^{(l)}*(outh^{(l-1)}))$
池化层
跟卷积层一样,我们先把 pooling 层也放回网络连接的形式中:
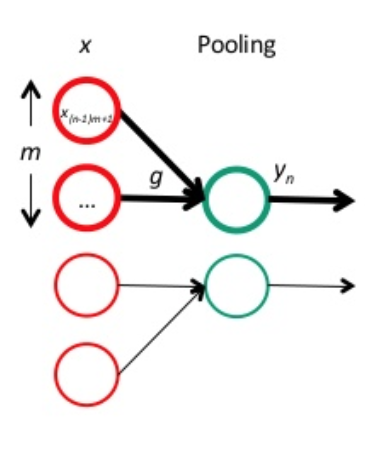
红色神经元是前一层的响应结果,一般是卷积后再用激活函数处理。绿色的神经元表示 pooling 层。
很明显,pooling 主要是起到降维的作用,而且,由于 pooling 时没有参数需要学习,
因此,当得到 pooling 层的误差项 $δ^l $后,我们只需要计算上一层的误差项 $δ^{l−1}$即可。
要注意的一点是,由于 pooling 一般会降维,因此传回去的误差矩阵要调整维度,即 upsample。这样,误差传播的公式原型大概是:
$\delta^{l-1}=upsample(\delta^l) \odot \sigma’(z^{l-1})$
下面以最常用的 average pooling 和 max pooling 为例,讲讲 $upsample(δ^l)$具体要怎么处理。
假设 pooling 层的区域大小为 2×22×2,pooling 这一层的误差项为:
$\delta^l= \left( \begin{array}{ccc} 2 & 8 \\ 4 & 6 \end{array} \right)$
首先,我们先把维度还原到上一层的维度:
$\left( \begin{array}{ccc} 0 & 0 & 0 & 0 \\ 0 & 2 & 8 & 0 \\ 0 & 4 & 6 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right)$
在 average pooling 中,我们是把一个范围内的响应值取平均后,作为一个 pooling unit 的结果。可以认为是经过一个 average() 函数,即 $average(x)=\frac{1}{m}\sum_{k=1}^m x_k$ 在本例中,$m=4$。则对每个 $x_k$ 的导数均为:
$\frac{\partial average(x)}{\partial x_k}=\frac{1}{m}$
因此,对 average pooling 来说,其误差项为:
$\begin{align} \delta^{l-1}=&\delta^l \frac{\partial average}{\partial x} \odot \sigma’(z^{l-1}) \notag \\ =&upsample(\delta^l) \odot \sigma’(z^{l-1}) \\ =&\left( \begin{array}{ccc} 0.5&0.5&2&2 \\ 0.5&0.5&2&2 \\ 1&1&1.5&1.5 \\ 1&1&1.5&1.5 \end{array} \right)\odot \sigma’(z^{l-1}) \end{align}$
在 max pooling 中,则是经过一个 max() 函数,对应的导数为:
$\frac{\partial \max(x)}{\partial x_k}=\begin{cases} 1 & if\ x_k=max(x) \ 0 & otherwise \end{cases}$
假设前向传播时记录的最大值位置分别是左上、右下、右上、左下,则误差项为:
$\delta^{l-1}=\left( \begin{array}{ccc} 2&0&0&0 \\ 0&0& 0&8 \\ 0&4&0&0 \\ 0&0&6&0 \end{array} \right) \odot \sigma’(z^{l-1}) $
总结:在遇到池化层的时间就执行upsampling的反向操作。就这样实现了池化层的反向传播。
这就是卷积神经网络的反向传播算法
转载请注明:Seven的博客

