神经网络入门-反向传播

反向传播（back propagation）算法推导

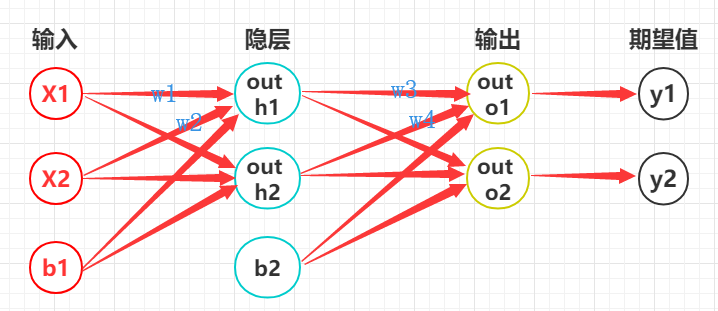
定义损失函数：

$E_{total}=\frac12 (y-outo)^2$

定义激活函数：

$\sigma(x)=sigmod(x) $

前向传播

第一层(输入层)：

• $x_1\ \ \ x_2\ \ \ b_1$

加权和：

• $net h_1=x_1w_1+x_2w_2+b_1$

第二层(隐层)：

• $outh_1=sigmod(neth_1)$

加权和：

• $neto_1=outh_1w_3+outh_2w_4+b_2$

第三层(输出层)：

• $outo_1=sigmod(neto_1)$

计算误差值：

• $Eo_1 = \frac12 (y_1-outo_1)^2$

• $Eo_2 = \frac12 (y_2-outo_2)^2$

• $E_{total}=Eo_1+Eo_2$

总结：要是使误差值最小，就需要误差反向传播算法，更新得到最小误差的权重参数w和b。

反向传播

须知：我们需要反向传递回去更新每一层对应的权重参数w和b。我们使用链式法则来反向模式求导。

更新第三层（输出层）的权重参数：

更新参数w：

$\frac{\partial E_{total}}{\partial w_3}=\frac{\partial E_{total}}{\partial outo_1} \cdot \frac{\partial outo_1}{\partial neto_1} \cdot \frac{\partial neto_1}{\partial w_3}$

$= \frac{\partial \frac12(y_1-outo_1)^2}{\partial outo_1} \cdot \frac{\partial sigmod(neto_1)}{\partial neto_1} \cdot \frac{\partial neto_1}{\partial w_3}$

$=(outo_1-y_1)\cdot outo_1(1-outo_1)\cdot outh_1$

$w_{3new}=w_{3old}-\eta \frac{\partial E_{total}}{\partial w_3}$， $\eta$是学习率

更新参数b：

$\frac{\partial E_{total}}{\partial b_2}=\frac{\partial E_{total}}{\partial outo_1} \cdot \frac{\partial outo_1}{\partial neto_1} \cdot \frac{\partial neto_1}{\partial b_2}$

$= \frac{\partial \frac12(y_1-outo_1)^2}{\partial outo_1} \cdot \frac{\partial sigmod(neto_1)}{\partial neto_1} \cdot \frac{\partial neto_1}{\partial b_2}$

$=(outo_1-y_1)\cdot outo_1(1-outo_1)$

$b_{2new}=b_{2old}-\eta \frac{\partial E_{total}}{\partial b_2}$， $\eta$是学习率

同理可得：w4：也就是同一层的w都可以用这种方式更新。

更新上一层(隐层)的权重参数：

更新权重参数w和b：

$\frac{\partial E_{total}}{\partial w_1}=\frac{\partial E_{total}}{\partial outh_1} \cdot \frac{\partial outh_1}{\partial neth_1} \cdot \frac{\partial neth_1}{\partial w_1}$

$\frac{\partial E_{total}}{\partial b_1}=\frac{\partial E_{total}}{\partial outh_1} \cdot \frac{\partial outh_1}{\partial neth_1} \cdot \frac{\partial neth_1}{\partial b_1}$

其中：

• $\frac{\partial E_{total}}{\partial outh_1} = \frac{\partial Eo_1}{\partial outh_1}+ \frac{\partial Eo_2}{\partial outh_1}$

• $\frac{\partial Eo_1}{\partial outh_1} = \frac{\partial Eo_1}{\partial neto_1} \cdot \frac{\partial neto_1}{\partial outh_1}$

• $ \frac{\partial Eo_1}{\partial neto_1} = \frac{\partial E_{o_1}}{\partial outo_1} \cdot \frac{\partial outo_1}{\partial neto_1} = (outo_1-y_1)\cdot outo_1(1-outo_1)$

• $ \frac{\partial neto_1}{\partial outh_1} = \frac{\partial (outh_1w_3+outo_2w_4+b_2)}{\partial outh_1} = w_3$

• 同理可得：

  • $\frac{\partial Eo_2}{\partial outh_1} = \frac{\partial Eo_2}{\partial neto_2} \cdot \frac{\partial neto_2}{\partial outh_1}$

  • $ \frac{\partial Eo_2}{\partial neto_2} = \frac{\partial E_{o_2}}{\partial outo_2} \cdot \frac{\partial outo_2}{\partial neto_2} = (outo_2-y_2)\cdot outo_2(1-outo_2)$

  • $ \frac{\partial neto_2}{\partial outh_1} = w_4$

综合上式：

$\frac{\partial E_{total}}{\partial w_1}= [w_3 (outo_1-y_1)\cdot outo_1(1-outo_1) + w_4(outo_2-y_2)\cdot outo_2(1-outo_2)] \cdot outh_1(1-outh_1) \cdot x_1$

$\frac{\partial E_{total}}{\partial b_1}= [w_3 (outo_1-y_1)\cdot outo_1(1-outo_1) +w_4(outo_2-y_2)\cdot outo_2(1-outo_2)] \cdot outh_1(1-outh_1) $

更新：

$w_{1new}=w_{1old}-\eta \frac{\partial E_{total}}{\partial w_1}$

$b_{1new}=b_{1old}-\eta \frac{\partial E_{total}}{\partial b_1}$

同理可得：w2：也就是同一层的w都可以用这种方式更新。

至此，我们所有的参数都更新完毕了，然后我们可以再次用新的参数进行前向传播，得到的误差就会是最小的

推广:

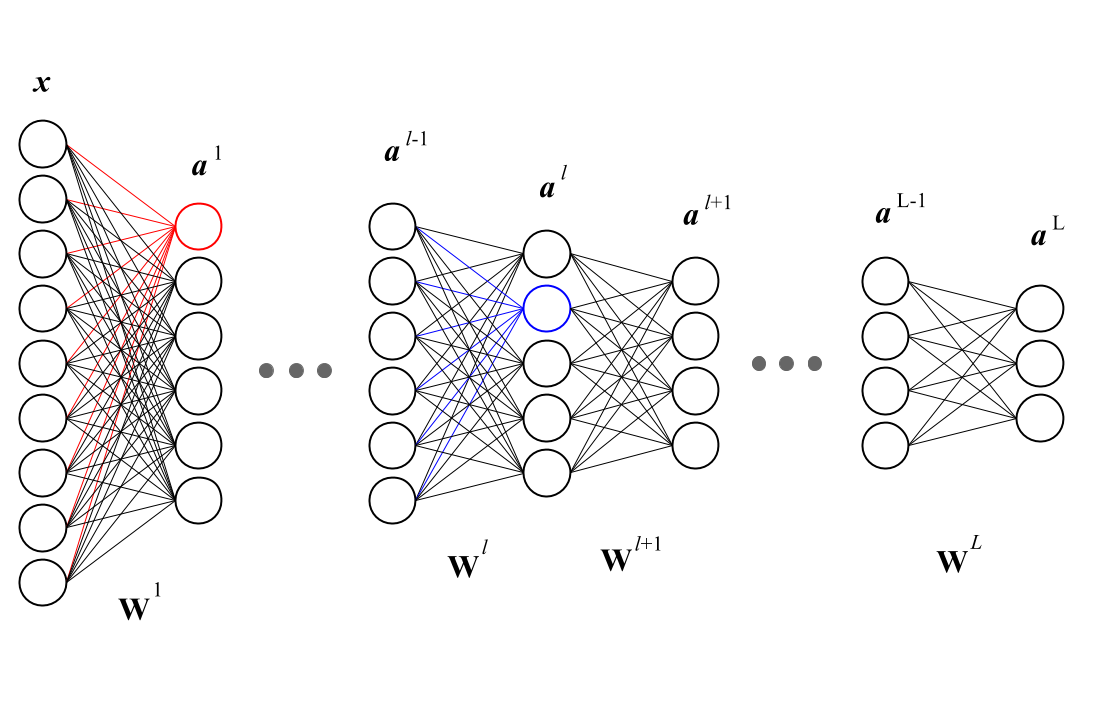
我们定义第L层的第i个神经元更新权重参数时(上标表示层数，下标表示神经元)：

• $\frac{\partial E_{total}}{\partial net_i^{(L)}} = \delta_i^{(L)}$

• $\frac{\partial E_{total}}{\partial w_{ij}^{(l)}}=outh_j^{(l-1)}\delta_i^{(l)}$ ，其中$w_{ij}^{(l)}$表示第$l$层的第$i$个神经元连接第$l-1$层的第$j$的神经元的相连的权重参数w。如下图所示：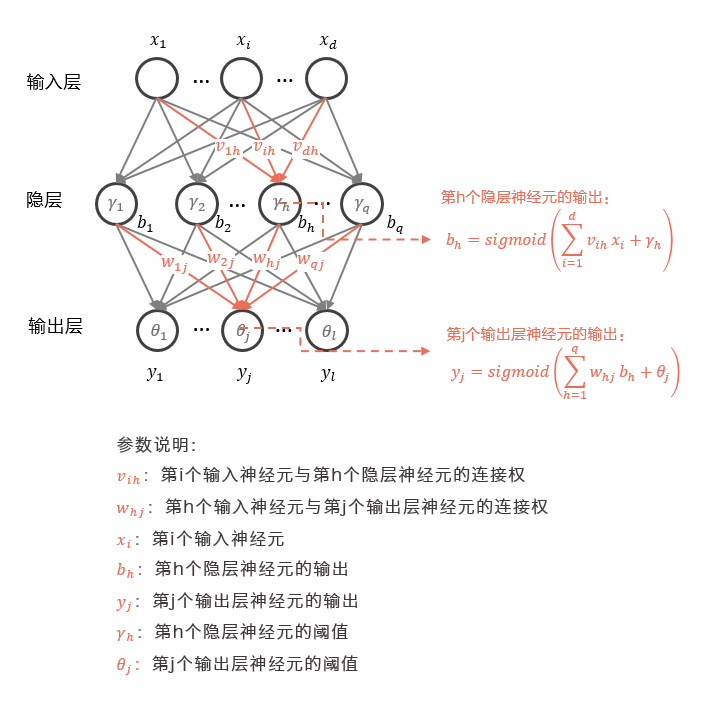

  

推广总结：

根据前面我们所定义的：

$E_{total}=\frac12 (y-outo)^2$

$\sigma(x)=sigmod(x) $

$\frac{\partial E_{total}}{\partial w_{ij}^{(l)}}=outh_j^{(l-1)}\delta_i^{(l)}$

$\delta_i^{(L)}=\frac{\partial E_{total}}{\partial net_i^{(L)}} $

$= \frac{\partial E_{total}}{\partial outh_i} \cdot \frac{\partial outh_i}{\partial net_i^{(L)}}$

$= \bigtriangledown_{out} E_{total} \times \sigma^{\prime}(net_i^{(L)})$

对于第$l$层：

$\delta^{(l)}=\frac{\partial E_{total}}{\partial net^{(l)}} $

$= \frac{\partial E_{total}}{\partial net^{(l+1)}} \cdot \frac{\partial net^{(l+1)}}{\partial net^{(l)}}$

$= \delta^{(l+1)} \times \frac{\partial net^{(l+1)}}{\partial net^{(l)}}$

$= \delta^{(l+1)} \times \frac{\partial (w^{(l+1)}\sigma (net^{(l)}))}{\partial net^{(l)}}$

$= \delta^{(l+1)} w^{(l+1)} \sigma^{\prime}(net^{(L)})$

对于偏置项bias：

$\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\delta_i^{(l)}$

反向传播的四项基本原则：

基本形式:

• $\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \times \sigma^{\prime}(net_i^{(L)}) $

• $\delta^{(l)} = \sum_j \delta_j^{(l+1)} w_{ji}^{(l+1)} \sigma^{\prime}(net_i^{(l)})$

• $\frac{\partial E_{total}}{\partial bias_i^{(l)}}=\delta_i^{(l)}$

• $\frac{\partial E_{total}}{\partial w_{ij}^{(l)}}=outh_j^{(l-1)}\delta_i^{(l)}$

矩阵形式：

• $\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \bigodot \sigma^{\prime}(net_i^{(L)}) $ ， $\bigodot$是Hadamard乘积（对应位置相乘）

• $\delta^{(l)} = (w^{(l+1)})^T \delta^{(l+1)} \bigodot \sigma^{\prime}(net^{(l)})$

• $\frac{\partial E_{total}}{\partial bias^{(l)}}=\delta^{(l)}$

• $\frac{\partial E_{total}}{\partial w^{(l)}}=\delta^{(l)}(outh^{(l-1)})^T$

当然如果你对具体推导不是很明白，你把这四项基本原则搞清楚，就可以直接使用了。

举个栗子

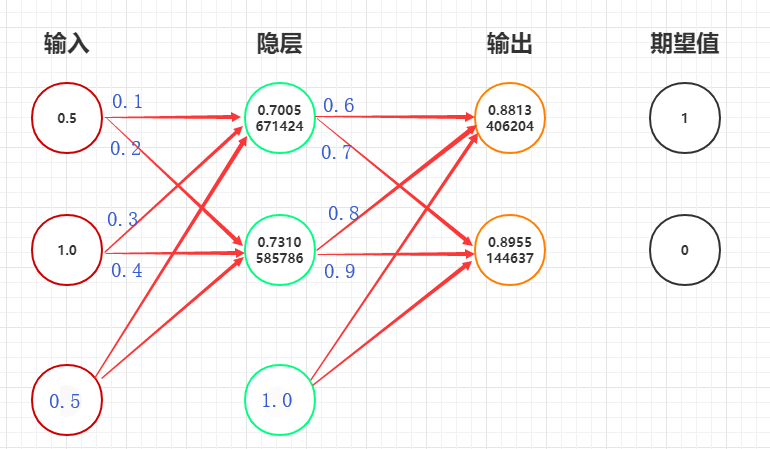
• 因为：$\delta_i^{(L)}= \bigtriangledown_{out} E_{total} \bigodot \sigma^{\prime}(net_i^{(L)}) $

  所以：

  $\delta^{(2)}= (out-y)\bigodot out(1-out)$

  $=(\begin{bmatrix} 0.88134 \\ 0.89551 \end{bmatrix} -\begin{bmatrix} 1 \\ 0 \end{bmatrix}) \bigodot (\begin{bmatrix} 0.88134 \\ 0.89551 \end{bmatrix} \bigodot (\begin{bmatrix} 1 \\ 1 \end{bmatrix}-\begin{bmatrix} 0.88134 \\ 0.89551 \end{bmatrix})) $

  $=\begin{bmatrix} -0.01240932\\ 0.08379177\end{bmatrix}$

• 因为：$\delta^{(l)} = (w^{(l+1)})^T \delta^{(l+1)} \bigodot \sigma^{\prime}(net^{(l)})$

  所以：

  $\delta^{(1)} = (w^{(2)})^T \delta^{(2)} \bigodot \sigma^{\prime}(net^{(1)})$

  $=(\begin{bmatrix} 0.6 & 0.8 \\ 0.7 & 0.9\end{bmatrix}^T \cdot \begin{bmatrix} -0.01240932\\ 0.08379177\end{bmatrix}) \bigodot \begin{bmatrix} 0.20977282 \\ 0.19661193\end{bmatrix}$

  $=\begin{bmatrix} 0.01074218\\ 0.01287516\end{bmatrix}$

• 因为：$\frac{\partial E_{total}}{\partial w^{(l)}}=\delta^{(l)}(outh^{(l-1)})^T$

  所以：

  $\Delta w^{(2)} = \delta^{(2)}(outh^{(1)})^T$

  $=\begin{bmatrix} -0.01240932\\ 0.08379177\end{bmatrix} \cdot \begin{bmatrix} 0.70056714\\ 0.73105858 \end{bmatrix}^T$

  $= \begin{bmatrix} -0.00869356 & -0.00907194 \\ 0.5870176 & 0.612567 \end{bmatrix}$

  $\Delta w^{(1)} = \delta^{(1)}x^T$

  $=\begin{bmatrix} 0.01074218\\ 0.01287516\end{bmatrix} \cdot \begin{bmatrix} 0.5\\ 1\end{bmatrix}^T$

  $= \begin{bmatrix} 0.00537109& 0.01074218\\ 0.00643758 & 0.01287516 \end{bmatrix}$

• 权重更新

  $w_{new}^2 = w_{old}^2-\Delta w^{(2)}$

  $= {\begin{bmatrix} 0.6 & 0.8 \\ 0.7 & 0.9\end{bmatrix}}-\begin{bmatrix} -0.00869356 & 0.00907194 \\ 0.5870176 & 0.612567 \end{bmatrix}$

  $= \begin{bmatrix} 0.60869356 & 0.80907194 \\ 0.64129824& 0.8387433 \end{bmatrix}$

  $b_{new}^2=b_{old}^2-\Delta b^2$

  $= \begin{bmatrix} 1 \\ 1 \end{bmatrix}-\begin{bmatrix} -0.01240932\\ 0.08379177\end{bmatrix}$

  $=\begin{bmatrix} 1.01240932\\ 0.91620823\end{bmatrix}$

  $w_{new}^1= w_{old}^1-\Delta w^{(1)}$

  $=\begin{bmatrix} 0.1 & 0.3 \\ 0.2 & 0.4\end{bmatrix} - \begin{bmatrix} 0.00537109& 0.01074218\\ 0.00643758 & 0.01287516 \end{bmatrix}$

  $= \begin{bmatrix} 0.09462891& 0.28925782\\ 0.19356242& 0.38712484\end{bmatrix}$

  $b_{new}^1=b_{old}^1-\Delta b^1$

  $=\begin{bmatrix} 0.5 \\ 0.5 \end{bmatrix} - \begin{bmatrix} 0.01074218\\ 0.01287516\end{bmatrix}$

  $=\begin{bmatrix} 0.48925782\\ 0.48712484\end{bmatrix}$

就这样，我们就完成了一个简单神经网络的误差反向传播进行权重参数更新

权重初始化

转载请注明：Seven的博客