EM算法简介
最大期望演算法(Expectation-maximization algorithm,又译期望最大化算法)在统计中被用于寻找,依赖于不可观察的隐性变量的概率模型中,参数的最大似然估计。
在统计计算中,最大期望(EM)算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。最大期望算法经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
最大似然估计
注意:EM算法主要用于从不完整数据中计算最大似然估计,本身可以看成是特殊情况下计算极大似然的一种方法。
极大似然估计所要解决的问题是:给定一组数据和一个参数待定的模型,如何确定模型的参数。使得这个确定的参数后的模型在所有模型中产生已知数据的概率最大。(模型已定,参数未知)。
简单举个例子:
- 10次抛硬币的结果是:正正反正正正反反正正
- 假设P是每次抛硬币的结果为正的概率。
- 得到这样实验结果的概率我们就可以算出来:
- $P=pp(1-p)ppp(1-p)(1-p)pp \\ = p^7(1-p)^3$
- 然后很愉快的最优解就算出来了:$p=0.7$
我们引申到二项分布的最大似然估计
- 在抛硬币的试验中,进行N次独立试验,n次朝上,N-n次朝下。
- 然后假定朝上的概率为p,使用对数似然函数作为目标函数:
- $f(n | p)=log(p^n(1-p^{N-n}))$
- $\frac{\partial(f(n | p))}{\partial p}=\frac nP-\frac{N-n}{1-p}=0$
- 然后就可以得到概率:$p=\frac nN$
升级一下,进一步考察
若给定有一组样本$x_1,x_2,…x_n$,已知它们来自于高斯分布$N(u,\sigma)$,试估计参数$u, \sigma$.
高斯分布的概率密度函数:
将$X_i$的样本值$x_i$带入,得:
化简对数似然函数:
$l(x)=log\prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-u)^2}{2\sigma^2}} \\ = \sum_ilog\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-u)^2}{2\sigma^2}} \\ =\sum_ilog\frac{1}{\sqrt{2\pi}\sigma} + \sum_i {-\frac{(x_i-u)^2}{2\sigma^2}} \\ =-\frac n2log(2\pi\sigma^2)-\frac{1}{2\sigma^2}\sum_i(x_i-u)^2 $
参数估计
到现在,我们就可以很直观的看出,这个结果是和矩估计的结果是一致的,也就是说样本的均值就是高斯分布的均值,样本的伪方差就是高斯分布的方差。
这就是我们所熟知的极大似然估计。
Jensen 不等式
设$f$是定义域为实数的函数,如果对于所有的实数$x$。如果对于所有的实数$x$,$f(x)$的二次导数大于等于0,那么$f$是凸函数。当$x$是向量时,如果其$hessian$矩阵$H$是半正定的,那么$f$是凸函数。如果只大于0,不等于0,那么称f是严格凸函数。
Jensen不等式表述如下:
如果$f$是凸函数,X是随机变量,那么:$E[f(X)]>=f(E[X])$
特别地,如果$f$是严格凸函数,当且仅当X是常量时,上式取等号。
如果用图表示会很清晰:
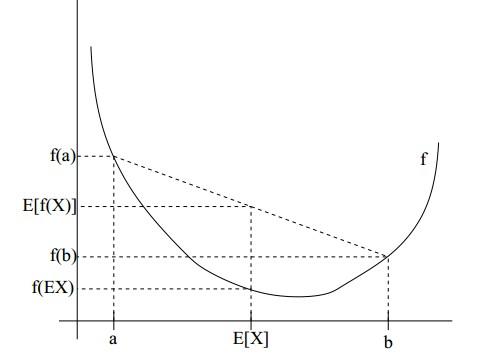
图中,实线$f$是凸函数,$X$是随机变量,有0.5的概率是a,有0.5的概率是b。(就像掷硬币一样)。X的期望值就是a和b的中值了,图中可以看到$E[f(X)]>=f(E[X])$成立。
当f是(严格)凹函数当且仅当-f是(严格)凸函数。
Jensen不等式应用于凹函数时,不等号方向反向。
如何理解EM算法?
在前面我们所遇到的,一堆由已知分布得到的数据,如果模型中的变量都是可以观测到了,为了求其中的参数,这时就可以直接使用极大似然估计。
但是,有这么一种情况,就是当模型中含有隐变量(数据观测不到了)的时候,再使用极大似然估计的时候,计算过程就会显得极为复杂甚至不可解。当我们正一筹莫展的时候,EM算法就出现了。
EM算法的思路
输入:观测变量数据X,隐变量数据Z,联合分布$P(X,Z | \theta)$,条件分布$P(Z | X,\theta)$
输出:模型参数$\theta$

未完待续

