上一节线性回归-算法推导 , 我们已经大致的知道了,线性回归的算法推导过程,但是往往我们在使用线性回归算法的过程中模型会出现过拟合的现象, 我们现从例子来看看什么是过拟合。
还是以房价预测为例,来看几张张图片:
1.欠拟合(Underfitting)
上图中,我们用$h_\theta(x)=\theta_0+\theta_1x $来拟合训练集中的数据,但是我们可以很明显的从图中看出,房价是不会随着面积成比例的增长的,这种情况,我们就称之为欠拟合。
2.过拟合(Overfitting)
如上图所示,我们用一条高次的曲线 $h_θ(x)=θ_0+θ_1x+θ_2x^2+θ_3x^3+θ_4x^4$ 来拟合训练集中的数据,因为参数过多,对训练集的匹配度太高、太准确,以至于在后面的预测过程中可能会导致预测值非常偏离合适的值,预测非常不准确,也就是说能力太强了,导致震荡的非常强烈。这就是过拟合。
3.合适的拟合(Properfitting)
如上图,如何参数选择的恰当,选用一个合适的曲线,比如说是$h_θ(x)=θ_0+θ_1x+θ_2x^2$来拟合上面的数据集就非常适合,这样这就是一个比较恰当的假设参数(hypothesis function).
简单总结一下
一般在实际的应用中是不会遇到欠拟合的情况的,但是过拟合是经常出现的,一般情况下,过拟合(Overfitting)就是:如果我在训练一个数据集的时候,用了太多的特征(features)来训练一个假设函数,就会造成匹配度非常高(误差几乎就为0, 也就是我上一节得出的损失函数:$ J(θ)=∑_N^{i=1}(y_i−θ^Tx_i)^2$),但是不能推广到其他的未知数据上,也就是对于其他的训练集是没有任何用的,不能做出正确的预测。
所以为了避免这种过拟合现象的发生,我们也有对应得惩罚,让他的能力不要那么强,所以就有L1(LASSO)、岭回归L2(Ridge)。我们来直观的了解下这两种正则。
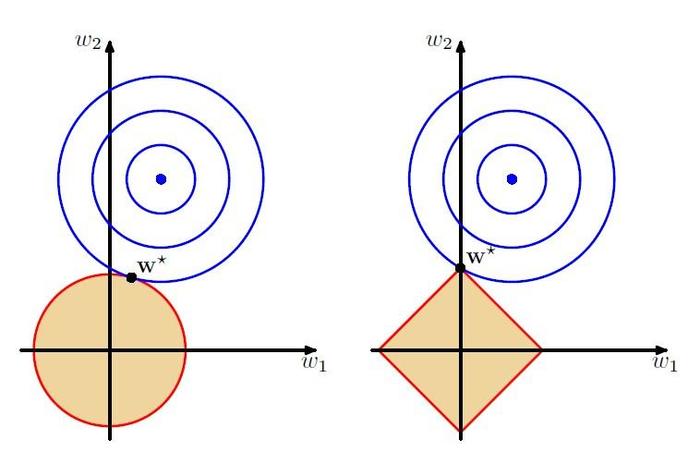
最小均方函数导数不为0时,L2导数加上最小均方函数导数肯定不为0。但是L1的正则项是绝对值函数,导数为0只要在x从左边趋向于0和从右边趋向于0时导数异号就行,所以更容易得到稀疏解。
目标函数最小均方差解空间为同心圆,L2解空间也为同心圆,L1解空间为菱形,两个解空间相交处为最优值。如图所示。
数学推导
总结上节的知识点,我们就有三种方式解出线性回归算法的表达式或解析解:
- 最小二乘法的解析解可以用高斯分布(Gaussian)以及最大似然估计法求得
- 岭回归Ridge(L2正则)的解析解可以用高斯分布(Gaussian)以及最大后验概率解释
- LASSO(L1正则)的解释解可以用拉普拉斯(Laplace)分布以及最大后验概率解释
在推导之前:
- 假设你已经懂得:高斯分布,拉普拉斯分布,最大似然估计,最大后验估计
- 机器学习的三要素:模型、策略、算法(李航《统计学习方法》)。就是说,一种模型可以有多种求解策略,每一种求解策略可能又有多种计算方法。所以先把模型策略搞懂,然后算法。
线性回归模型总结
首先我们先假设线性回归模型:
$f(x)= \sum_{i=1}^nx_iw_i+b=w^TX+b$
其中$x \in R^{1\times n}, w\in R^{1\times n},当前已知:X=(x_1 \cdot \cdot \cdot x_m) \in R^{m\times n}, y \in R^{n\times 1}, b \in R$,求出$w$
最小二乘法
如果$b \sim N(u, \sigma^2)$, 其中$u=0$, 也就是说$y_i \sim N(w^TX,\sigma^2)$
采用最大似然估计法:
$L(w)=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-w^Tx_i)^2}{2\sigma^2})}$
对数似然函数:
$l(w)=-nlog\sigma\sqrt{2\pi}-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2 $
因为我们要求的是似然函数的最大值:
$arg max_w \ L(w)=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-w^Tx_i)^2}{2\sigma^2})}$
通过对数似然进行变换后,因为$-nlog\sigma\sqrt{2\pi}$是定值,所以最终解析解:
$arg min_w f(w)=\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2 =||y-w^TX||_2^2$
岭回归Redge(L2正则)
如果$b \sim N(u, \sigma^2), w_i \sim N(u, \tau^2)$,其中$u=0$;
所以使用最大后验估计推导:
构建似然函数:
$L(w)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-w^Tx_i)^2}{2\sigma^2})} \cdot \prod_{j=1}^{d}\frac{1}{\sqrt{2\pi}\tau}e^{-(\frac{(w_j)^2}{2\tau^2})}$
对数似然函数
$l(w)=-nln\sigma\sqrt{2\pi}-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2 -dln \tau \sqrt{2\pi}-\frac{1}{2\tau^2}\sum_{j=1}^{d}(w_j)^2 $
因为$-nln\sigma\sqrt{2\pi}-dln \tau \sqrt{2\pi}$是定值,最后的解析解:
$arg max_w \ L(w) = arg min_w f(w)=\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2+ \lambda\sum_{j=1}^{d}(w_j)^2 \\ =||y-w^TX||_2^2+\lambda||w||_2^2 $
LASSO(L1正则)
如果$b \sim N(u, \sigma^2), w_i \sim Laplace(u,b)$,其中$u=0$;
所以使用最大后验估计推导:
构建似然函数:
$L(w)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-w^Tx_i)^2}{2\sigma^2})} \cdot \prod_{j=1}^{d}\frac{1}{2b}e^{-(\frac{|w_i|}{b})}$
对数似然:
$l(w)=-nln\sigma\sqrt{2\pi}-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2 -dln 2b -\frac{1}{b}\sum_{j=1}^{d}|w_j| $
因为$-nln\sigma\sqrt{2\pi}-dln2b$是定值,最后的解析解:
$arg max_w \ L(w) = arg min_w f(w)=\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-w^Tx_i)^2+ \lambda\sum_{j=1}^{d}|w_j| \\ =||y-w^TX||_2^2+\lambda||w||_1$
线性回归正则化总结
L1正则化和L2正则化可以看做是损失函数的惩罚项,所谓『惩罚』是指对损失函数中的某些参数做一些限制 ,都能防止过拟合,一般L2的效果更好一些,L1能够产生稀疏模型,能够帮助我们去除某些特征,因此可以用于特征选择。
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择

